[Real MySQL 8.0] 인덱스 살펴보기 1/2
인덱스는 컬럼의 값과 해당 레코드가 저장된 주소를 키와 값의 쌍으로 삼아 주어진 순서로 미리 정렬해 저장해 두고 원하는 결과를 최대한 빠르게 찾아갈 수 있도록 한다.
인덱스를 쉽게 설명해 책으로 비유하자면 색인으로 설명할 수 있다.
책의 색인을 통해 알아낼 수 있는 페이지 번호는 데이터 파일에 저장된 레코드의 주소에 비유될 것이고, 해당 페이지의 내용은 데이터 파일에 비유할 수 있다.
또 색인과 DBMS 인덱스의 중요한 공통점은 바로 정렬이다.
색인의 내용이 너무 많으면 원하는 검색어를 찾아내는데 시간이 걸릴 것이다.
이때 색인의 정보가 정렬이 되어있다면(ㄱ, ㄴ, ㄷ, …) 원하는 정보를 최대한 빠르게 찾아갈 수 있다. 인덱스도 마찬가지로 컬럼의 값을 주어진 순서로 미리 정렬해서 보관하므로 원하는 결과를 최대한 빠르게 찾아갈 수 있다.
인덱스 사용 목적
DBMS에서 테이블의 모든 데이터를 검색해서 원하는 결과를 가져오려면 시간이 오래 걸린다. 따라서 인덱스를 생성해놓고 이 시간을 단축시키는 것이 목적이다. 즉, 데이터의 읽기 속도를 높이는 기능으로 볼 수 있다.
읽기 속도는 향상되지만 데이터의 추가나 삭제 시 인덱스 또한 재정렬 과정을 거쳐야하므로 INSERT, UPDATE, DELETE와 같은 데이터 저장 성능은 떨어질 수밖에 없다. 따라서 무분별한 인덱스 추가는 지양해야 하며 저장 속도를 얼마나 희생할지, 읽기 속도를 얼마나 더 빠르게 만들어야 하는지에 따라 인덱스의 추가 여부를 결정해야 한다.
인덱스의 역할별 구분
- 프라이머리 키
- 레코드를 대표하는 컬럼의 값으로 만들어진 인덱스를 의미한다.
- 해당 레코드를 식별할 수 있는 값이기 때문에 식별자라고도 부른다.
- Null을 허용하지 않으며 중복을 허용하지 않는다.
- 보조 키(세컨더리 인덱스)
- 프라이머리 키를 제외한 나머지 모든 인덱스는 세컨더리 인덱스로 분류한다.
- 유니크 인덱스는 프라이머리 키와 비슷하고 프라이머리 키를 대체해 사용할 수 있어 대체 키라고도 부른다.
인덱스의 알고리즘 별 구분
- B-Tree 인덱스
- 가장 일반적으로 사용되는 인덱스 알고리즘으로, 오래전부터 도입된 알고리즘이기 때문에 성숙도가 높음
- 컬럼의 값을 변형하지 않고 원래의 값을 이용해 인덱싱하는 알고리즘
- B-Tree의 응용 버전으로 R-Tree 인덱스가 있다.
- Hash 인덱스
- 컬럼의 값으로 해시값을 계산해서 인덱싱하는 알고리즘
- 매우 빠른 검색을 지원한다.
- 값을 변형해서 인덱싱하므로 prefix 일치와 같이 값의 일부만 검색하거나 범위 검색 시 Hash 인덱스를 사용할 수 없다.
- 메모리 기반의 DB에서 많이 사용한다.
B-Tree 인덱스
인덱싱 알고리즘 가운데 가장 일반적으로 사용되고, 가장 먼저 도입된 알고리즘으로 범용적인 목적으로 사용되는 인덱스 알고리즘이다. 컬럼의 값을 변형시키지 않고 인덱스 구조체 내에서 항상 정렬된 상태로 유지된다. 일반적으로 DMBS에서는 B-Tree의 변형 알고리즘인 B+-Tree 또는 B*-Tree가 사용된다.
B-Tree 인덱스는 Balanced-Tree를 의미한다. Binary가 아닌 것에 주의하자.
구조 및 특성

B-Tree는 트리 구조의 최상위에 하나의 루트 노드가 존재하고 그 하위에 자식 노드가 붙어있는 구조를 가지고 있다. 가장 하위의 노드를 “리프 노드(Leaf node)”라 하고, 루트 노드도 리프 노드도 아닌 중간의 노드를 “브랜치 노드”라고 한다.
인덱스의 리프 노드는 실제 데이터 레코드를 찾아가기 위한 주솟값을 가지고 있으며, 인덱스의 키 값은 모두 정렬되어 있지만 데이터 파일의 레코드는 임의의 순서로 저장돼 있다. (Insert 되고 Delete 되는 과정 때문에 빈 공간이 생김)
InnoDB 테이블의 인덱스와 데이터 파일의 관계
InnoDB 스토리지 엔진을 사용하는 테이블에서는 프라이머리 키가 ROWID의 역할(물리적 주솟값)을 한다.
하지만 세컨더리 인덱스는 프라이머리 키를 주소처럼 사용하기 때문에 물리적인 주소가 아닌 논리적인 주소를 가진다고 볼 수 있다.
따라서 InnoDB 테이블에서 인덱스를 통해 레코드를 읽을 때는 데이터 파일을 바로 찾아가지 못하고 다음과 같은 과정을 거친다.

인덱스에 저장돼 있는 프라이머리 키 값을 이용해 프라이머리 키 인덱스를 한번 더 검색한 후, 프라이머리 키 인덱스의 리프 페이지에 저장돼 있는 레코드를 읽는다. 즉, 모든 세컨더리 인덱스 검색에서 프라이머리 키를 저장하고 있는 B-Tree를 한번 더 검색해야만 데이터 레코드를 읽을 수 있다.
B-Tree 인덱스 키 추가 및 삭제
테이블에 레코드를 저장하거나 변경하는 경우 인덱스 키 추가나 삭제 작업이 발생한다. 이러한 키 추가나 삭제가 어떻게 처리되는지 알아두면 쿼리 성능을 쉽게 예측할 수 있다.
인덱스 키 추가
- 새로운 키 값이 B-Tree에 저장될 때는 저장될 키 값을 이용해 B-Tree상의 적절한 위치를 검색
- 저장될 위치가 결정되면 레코드의 키 값과 레코드의 주소 정보를 B-Tree 리프 노드에 저장
- 만약 리프 노드가 꽉 차서 더는 저장할 수 없는 경우 리프 노드를 분리
- 리프 노드가 분리되는 경우 상위 브랜치 노드까지 처리해줘야 함(상대적으로 쓰기 작업의 비용이 상승)
인덱스 추가 시 계략적 비용 계산
앞서 언급했듯, 인덱스 추가가 INSERT나 UPDATE 문장에 어떤 영향을 줄지 쿼리 성능을 예측하고 싶어 하는 사람이 많다. 이를 명확하게 답하려면 테이블 컬럼 수, 컬럼의 크기, 인덱스 컬럼의 특성 등을 확인해야 한다.
계략적으로 계산하는 방법은 테이블에 레코드 추가 비용을 1이라고 가정하고 해당 테이블의 인덱스 추가 작업 비용을 1.5 정도로 예측하는 것이다.
예를 들어, 테이블에 인덱스가 3개 있다면 인덱스가 하나도 없는 경우는 작업 비용이 1이고 3개인 경우 5.5(1.5 * 3 + 1) 정도의 비용이 드는 것으로 예측한다. (디스크로부터 인덱스 페이지를 읽고 쓰기를 하는데 걸리는 비용)
인덱스 키 삭제
- 키 값이 저장된 B-Tree 리프 노드를 검색
- 삭제 마크 추가(디스크 I/O 필요)
- 버퍼링되어 지연 처리 가능
인덱스 키 변경
- B-Tree 키 값을 삭제 (인덱스 키 삭제)
- 다시 새로운 키 값을 추가 (인덱스 키 추가)
- 체인지 버퍼를 이용해 지연 처리 가능
인덱스 키 검색
인덱스 검색 작업은 B-Tree 루트 노드부터 브랜치 노드를 거쳐 리프 노드까지 이동하면서 비교 작업을 수행한다. 이 과정을 “트리 탐색"이라고 하며, 인덱스 트리 탐색은 SELECT뿐 아니라 UPDATE나 DELETE를 처리하기 위해 레코드를 먼저 검색할 때도 사용된다.
다음은 B-Tree 인덱스를 이용한 키 검색이 가능한 경우와 불가능한 경우를 나타낸다.
- 100% 일치(동등 연산, = ‘test') 또는 값의 앞부분만 일치하는 경우(LIKE 연산, “test%”) 사용 가능
- 부등호 (< , >) 비교 조건에서 사용 가능
- 키 값의 뒷부분만 검색하는 경우(LIKE 연산, “%test”) 사용 불가능
- 키 값에 변형이 가해지는 경우 사용 불가능
InnoDB 테이블에서 지원하는 레코드 잠금이나 넥스트 키락(갭 락)이 검색을 수행한 인덱스를 잠근 후 테이블의 레코드를 잠그는 방식으로 구현돼 있다. 따라서 UPDATE나 DELETE를 수행할 때 적절한 인덱스가 없으면 불필요하게 많은 레코드를 잠근다. 따라서 InnoDB 스토리지 엔진에서는 인덱스 설계가 굉장히 중요하고 많은 부분에 영향을 미친다.
B-Tree 인덱스 사용에 영향을 미치는 요소
B-Tree 인덱스는 인덱스를 구성하는 컬럼의 크기와 레코드 건수, 유니크한 인덱스 키 값의 개수 등에 검색이나 변경 작업의 성능이 영향을 받는다. 인덱스의 키 값의 크기를 작게 하거나 유니크한(중복도가 낮은) 값으로 만들면 인덱스 성능이 좋아진다.
인덱스 키 값의 크기
인덱스는 다음과 같이 페이지 단위로 관리된다.
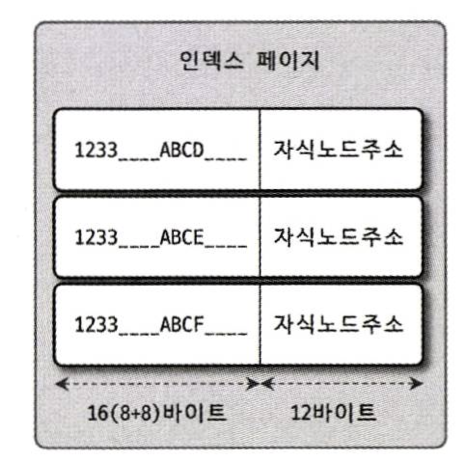
따라서 인덱스의 페이지 크기와 키 값의 크기에 따라 B-Tree가 자식 노드를 몇 개까지 가질 수 있는지 결정된다.
그렇다면 16KB짜리 인덱스 페이지가 몇 개의 키를 저장할 수 있을까?
위 그림처럼 16 * 1024 / (16(키 값의 크기) + 12(자식 노드 주소 크기)) = 585 개의 키를 저장할 수 있다. 이때, 키 값이 두 배인 32Byte로 늘어났다고 가정하면 16 * 1024 / (32(키 값의 크기) + 12(자식노드 주소 크기)) = 372개 저장할 수 있다.
예를 들어, 500개의 레코드를 읽을 때 키 값이 16바이트인 인덱스 페이지는 디스크를 한 번만 읽으면 되지만, 키 값이 32바이트인 인덱스 페이지는 디스크를 두 번 읽어야 한다. 즉, 키 값이 커지면 디스크를 읽어야 하는 횟수가 늘어나고 그만큼 느려진다.
인덱스 크기가 커지면 커질수록 메모리에 캐시 해 둘 수 있는 레코드 수는 줄어들기 때문에 자연히 메모리 효율이 떨어지는 결과를 가져온다.
B-Tree 깊이
B-Tree 깊이는 앞서 살펴본 인덱스 키 값의 평균 크기와 관계가 있다.
B-Tree 깊이가 3인 경우를 예로 들어 설명해보자면, 키 값이 16바이트인 경우 최대 2억(585 * 585 * 585)개 정도의 키 값을 담을 수 있지만, 32바이트인 경우 담을 수 있는 키 값이 5천만(372 * 372 * 372)개로 줄어든다.
인덱스 키 값의 크기가 커질수록 인덱스 키 값의 개수가 적어지고 B-Tree의 깊이도 깊어진다. B-Tree의 깊이는 값을 검색할 때 몇 번이나 랜덤 I/O를 수행해야 하는지와 직결되는 문제로, 깊이가 깊을수록 디스크 읽기가 많아진다.
선택도(기수성)
선택도(Selectivity) 또는 기수성(Cardinality)은 거의 같은 의미로 사용되며, 모든 인덱스 키 값 가운데 유니크한 값의 수를 의미한다. 인덱스 키 값 가운데 중복된 값이 많아지면 기수성은 낮아지고 선택도 또한 떨어진다.
선택도(기수성)는 인덱스 성능에 큰 영향을 미치는 요소이며 선택도가 높을수록 검색 대상이 줄어들기 때문에 그만큼 빨리 처리된다. 전체 레코드 건수를 유니크한 값의 개수로 나눠보면 하나의 키 값으로 검색했을 때 대략 몇 건의 레코드가 일치할지 예측할 수 있다.
tb_city라는 테이블에 1만 건의 국가와 도시가 중복해서 저장돼 있지 않고 country 컬럼에만 인덱스가 준비돼 있다고 가정해보자.
SELECT * FROM tb_city
WHERE country='KOREA' AND city='SEOUL';이제 위 쿼리를 실행했을 때, country 컬럼의 유니크 값 개수에 따라 인덱스의 효율성이 어떻게 달라지는지 살펴보자.
- country 칼럼의 유니크 값이 10개일 때
- country=’KOREA’ 라는 조건으로 인덱스를 검색하면 1만 건의 데이터 중 1,000건(10,000 / 10)의 데이터가 일치할 것이라 예상할 수 있다.
- city=’SEOUL’인 레코드는 1건이므로 1,000건 중 999건이 불필요하게 읽히는 것으로 볼 수 있다.
- country 칼럼의 유니크 값이 1,000개일 때
- country=’KOREA’ 라는 조건으로 인덱스를 검색하면 1만 건의 데이터 중 10건(10,000 / 1,000)의 데이터가 일치할 것이라 예상할 수 있다.
- city=’SEOUL’인 레코드는 1건이므로 10건 중 9건이 불필요하게 읽히는 것으로 볼 수 있다.
같은 쿼리를 실행해 같은 결과를 받았지만, MySQL 서버가 수행하는 작업 내용에는 차이가 크다는 것을 알 수 있다. 이처럼 인덱스에서 유니크한 값의 개수는 인덱스나 쿼리의 효율성에 큰 영향을 미친다.
읽어야 하는 레코드의 수
인덱스를 통해 테이블 레코드를 읽는 것은 인덱스를 거치지 않고 읽는 것보다 높은 비용이 드는 작업이다. 따라서 인덱스를 통해 레코드를 읽어오는 방법과 인덱스를 거치지 않고 읽어오는 방법 중 어느 것이 효율적인지 판단해야 한다.
일반적으로 읽어야 할 레코드 수가 전체 테이블 레코드의 20~25%를 넘어서면 테이블을 모두 직접 읽어서 필터링을 수행하는 것이 더 효율적이다.
예를 들어, 전체 100만 건의 레코드 가운데 50만 건을 읽어야 하는 작업은 전체 테이블의 50%를 읽는 작업이다. 즉, 손익 분기점인 20~25%보다 훨씬 크기 때문에 테이블 전체를 직접 읽는 것이 인덱스를 통해 읽는 것보다 더 효율적이다.